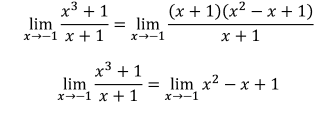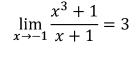 Una función continua es aquella para la cual, intuitivamente, para puntos cercanos del dominio se producen pequeñas variaciones en
los valores de la función. Si la función no es continua, se dice que es discontinua. Una función continua de en es aquella cuya
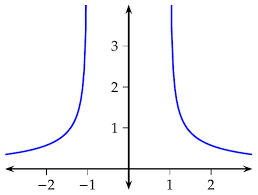
gráfica puede dibujarse sin levantar el lápiz del papel (más formalmente su grafo es un conjunto conexo).
Una función continua es aquella para la cual, intuitivamente, para puntos cercanos del dominio se producen pequeñas variaciones en
los valores de la función. Si la función no es continua, se dice que es discontinua. Una función continua de en es aquella cuya
gráfica puede dibujarse sin levantar el lápiz del papel (más formalmente su grafo es un conjunto conexo).La continuidad de funciones es uno de los conceptos principales del análisis matemático y de la topología. El artículo describe principalmente la continuidad de funciones reales de una variable real.
El límite de una función está íntimamente unido a su representación gráfica y a la interpretación de la misma debido a que lo que nos indica es el comportamiento o tendencia de la gráfica. Por esta razón, el concepto de límite es básico en el Análisis Matemático.
Las primeras definiciones de límite aparecen en la obra de Jonh Wallis (1616- 1703) y en ella se utiliza por primera vez el símbolo infinito. Con posterioridad Jean Le Rond D'Alembert perfeccionó la definición de límite. Fue Ausgustin Cauchy (1789-1857) quien dio la definición de límite que utilizamos hoy en día.